lunes, 28 de mayo de 2012
Funciones polinómicas:
Las funciones polinómicas son, como su nombre lo dice, funciones que constan de un polinomio.
en donde n es un entero positivo, llamado, grado del polinomio. Resulta evidente, que el coeficiente del grado mayor, no puede ser cero, o sea, a tiene que ser diferente de cero, para que el grado del polinomio se n. Cualquiera de los otros coeficientes puede ser cero.
Ejemplos de funciones polinómicas son:
La gráfica de las funciones polinómicas depende del grado de la función. Las funciones polinómicas de ciertos grados tienen ciertas alternativas de gráfica. Queda a este curso de derivadas averiguar algunas de las características de las funciones para poder predecir su comportamiento.
Muchas veces a partir de la gráfica de un polinomio se puede deducir la ecuación de la función. Ésto se puede hacer a partir de las intersecciones con los ejes. (Conste que comenté, que muchas veces, NO SIEMPRE).
Una función polinómica con el más alto número de intersecciones con el eje "x" permisible, es aquella que se puede determinar su gráfica y su ecuación.
Una función de, por ejemplo, tercer grado puede tener como máximo 3 intersecciones con el eje "x".
Una función de sexto grado puede tener como máximo 6 intersecciones con el eje "x".
Cabe aclarar, que las funciones polinómicas, aunque no conozcamos ahora los términos específcos, son funciones continuas,sin asíntotas verticales, ni horizontales, que según el grado pueden presentar máximos, mínimos y puntos de inflexión.
domingo, 27 de mayo de 2012
Función racional
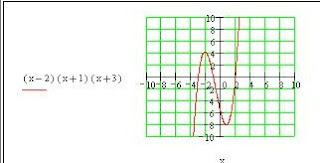
En matemáticas, una función racional es una función que puede ser expresada de la forma:
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
- Ejemplo
 si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.
si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.
- Toda función racional es de clase
 en un dominio que no incluya las raíces del polinomio Q(x).
en un dominio que no incluya las raíces del polinomio Q(x). - Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).
Integración de las Funciones
Dada una función racional:
Si el denominador es un polinómico mónico 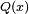 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
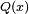 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
Si 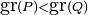 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
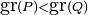 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
Por lo que la integral de la función  es una combinación lineal de funciones de la forma
es una combinación lineal de funciones de la forma  :
:
 es una combinación lineal de funciones de la forma
es una combinación lineal de funciones de la forma  :
:
Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la intergración.
Función polinómica
En matemáticas, una función polinómica es una función asociada a un polinomio con coeficientes en un anillo conmutativo (a menudo un cuerpo).
Formalmente, es una función:

- donde
 es un polinomio definido para todo número real
es un polinomio definido para todo número real  ; es decir, una suma finita de potencias de
; es decir, una suma finita de potencias de  multiplicados por coeficientes reales, de la forma:1
multiplicados por coeficientes reales, de la forma:1
Funciones polinomicas básicas:
Algunas funciones polinómicas reciben un nombre especial según el grado del polinomio:
| Grado | Nombre | Expresión |
|---|---|---|
| 0 | función constante | y = a |
| 1 | función lineal | y = ax + b es un binomio del primer grado |
| 2 | función cuadrática | y = ax² + bx + c es un trinomio del segundo grado |
| 3 | función cúbica | y = ax³ + bx² + cx + d es un cuatrinomio de tercer grado |
Funciones constantes
La función constante es del tipo:
y = n
El criterio viene dado por un número real.
La pendiente es 0.
La gráfica es una recta horizontal paralela a al eje de abscisas.

Rectas verticales
Las rectas paralelas al eje de ordenadas no son funciones, ya que un valor de x tiene infinitas imágenes y para que sea función sólo puede tener una. Son del tipo:
x = K

- abscisa Coordenada x de un punto en un sistema de coordenadas Cartesianas. Es la distancia horizontal de un punto al eje vertical, o y.


Función Lineal
Se la llama función lineal a toda función que cumple la forma:
f(x)= mx + b
Donde "m" es la pendiente de la X, y "b" es la variable independiente, que no depende de la X.
La gráfica de una función siempre es una recta. esta recta corta al eje de Y en un punto,
en el cual X vale 0, y este punto es igual a "b", o sea la variable independiente.
Por ejemplo:
f(x) = 3x + 2 f(0) = 3*0 + 2 f(0) = 2 ==> la recta corta al eye Y en punto (0;2)
y hacia qué lado va a estar inclinada.
Función Cuadrática
Una función cuadrática es de la forma:

- "a" es la variable dependiente del termino cuadrático,
- además es el término principal
- y a diferencia de las otras ésta no puede ser nula.
- "b" es la variable dependiente del termino lineal.
- "c" es el termino independiente,
- a su vez es la ordenada al origen, o sea, la f(0).
La gráfica de una función cuadrática es una parábola
y su representación es una curva como la imagen dada.
"a" modifica la abertura de la parábola,
si es negativo la parábola "mira para abajo"
y si es positiva "mira para arriba".
Esta función puede sufrir traslaciones.
Suscribirse a:
Entradas (Atom)














![f(x) = \frac{P(x)}{Q(x)}, \qquad P(x),Q(x)\in \R[x]](http://upload.wikimedia.org/wikipedia/es/math/8/e/4/8e418aac8dbe42c60615386abe8a0d10.png)