En matemáticas, una función racional es una función que puede ser expresada de la forma:
donde P y Q son polinomios y x una variable, siendo Q distinto del polinomio nulo. Las funciones racionales están definidas o tienen su dominio de definición en todos los valores de x que no anulen el denominador.
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
- Ejemplo
 si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.
si el denominador es distinto de cero, y si ad ≠ bc, la curva correspondiente es una hipérbola equilátera.
- Toda función racional es de clase
 en un dominio que no incluya las raíces del polinomio Q(x).
en un dominio que no incluya las raíces del polinomio Q(x). - Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).
Integración de las Funciones
Dada una función racional:
Si el denominador es un polinómico mónico 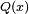 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
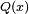 con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos de polinomio irreducibles:
Si 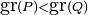 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
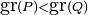 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
Por lo que la integral de la función  es una combinación lineal de funciones de la forma
es una combinación lineal de funciones de la forma  :
:
 es una combinación lineal de funciones de la forma
es una combinación lineal de funciones de la forma  :
:
Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la intergración.


![f(x) = \frac{P(x)}{Q(x)}, \qquad P(x),Q(x)\in \R[x]](http://upload.wikimedia.org/wikipedia/es/math/8/e/4/8e418aac8dbe42c60615386abe8a0d10.png)
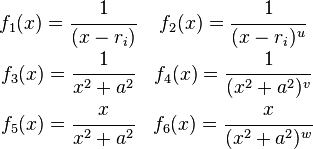

No hay comentarios:
Publicar un comentario